Pricing a raffle
19 Sep 2012
I’m selling our campervan.
It’s not going to raise a lot of money. But Matthew at work suggested a novel way of selling it, which got me thinking.
“Have a raffle,” he said, “two quid a ticket. Bet you could sell loads.”
I’m not sure about the legalities, and I am sure it’d be tricky to achieve a few hundred, small-but-traceable transactions (without sitting in town selling tickets), so I’m going to stick to the more conventional methods.
It did get me pondering though, and sparked an interesting discussion. In that situation, I’ve got something to sell and, supposing I want to maximise the amount of money I get for it, the only things I can control are:
- how many tickets I sell
- how much I charge for a ticket
- how hard I try to advertise my ‘raffle’
Assuming I maximise the advertising, how (mathematically) ought I to choose the other two variables in order to achieve maximum sales?
If we simplify the situation a bit - take out the subjective value of the ‘prize’ and let’s say I’m raffling £1000. The amount is important, I think, because people’s behaviour doesn’t scale: more people will whack a pound on an outside chance (National Lottery) than would bet their life savings on something with a higher probability - say, a 60% chance of doubling your stake.
I kept going round in circles trying to analyse it.
- If I raise the ticket price, it’ll put people off buying. At the same time, it’ll increase my takings per-ticket, and perhaps people will think “aha, he’s not going to sell many tickets”, so the perceived value of a ticket goes up again.
- Should I limit the number of tickets? That way, people can see their probability of winning and work out whether to buy or not. However, if I choose a high limit, there’s no guarantee of selling all the tickets.
- and so on
In the extreme, perhaps advertising the van for sale at x pounds is equivalent to limiting the number of tickets to one…
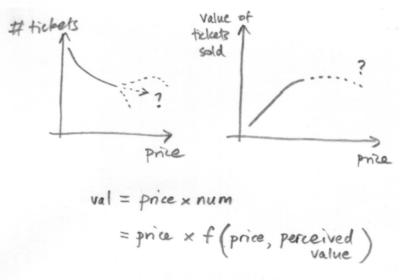
One thing is clear. Ignoring transaction costs etc., the amount of money I take is equal to ticket price multiplied by number sold.
The attached sketch is as far as I got. Assume that the number of people I can reach with my advertising is very large. Selling tickets for a ridiculously low price, I could expect to shift a lot of ‘em. As I raise the price, I expect the sales volume to decrease. But is there a turning point in the curve, a point where the increased ticket price actually reverses the demand curve because people think I’ll sell fewer?
Is there some simple analysis for this type of problem? Have I missed some clever way of looking at it, I wonder?
Tags: data, maths, campervan, game theory
< Previous post | Next post >Favourite posts
- On wiggly lines and being normal
- On infinite villages
- Running a race backwards
- Brainmaking
- Their tables were stored full, to glad the sight
- The structure of a smell
Recent posts
- Start your holidays with a meta-alarm
- PGN files from handwritten chess notation
- Souvenirs des villes européennes
- Pic'n'mix reinvented
- Super slow-mo Tetris
Blog archives
Posts from 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023, 2024.