Optimising the FA Cup

31 Jan 2023

The early rounds of the FA Cup are great fun to watch. This year I followed from the 3rd Qualifying Round. My team is Liverpool and they don’t even enter the competition until January (on current form, they may exit the competition before February). So instead, I like to follow a reasonably local team, but to provide some sort of journey through the Cup, without early termination, I pursue an unfaithful support-whoever-wins system.

This year, then, King’s Lynn went on a good run, but it came to an end in December when they were beaten 3-0 at home by Stevenage. It took a good few days to come around to the idea of supporting Stevenage, having spent 90 minutes cheering on their opposition, but they got a tasty 3rd round draw and caused a cup upset by winning at Villa Park.

This post is less about football and more about the interesting optimisation problem that I pondered during the drive to and from Birmingham. Given that I’ve chosen to start watching the cup at some stage, to which fixture should I go to optimise my enjoyment from following my support-whoever-wins system?

Let’s make some assumptions, all of which are false, but close enough and enable us to start to explore the ideas:

• define optimal as meaning the minimum time spent travelling to/from games. Real optimal would of course be my favourite local team winning the Cup, but we have to make some concessions for mathematical purposes.
• ignore the fact that the FA Cup is regional for the earlier rounds, and that semi-finals always happen at Wembley nowadays. I’m pretty much never going to get a ticket for that stage anyway.
• pretend that replays never happen.
• model each game as a 50-50 random win for either home team or away team.

Intuitively, I expect that going as a home supporter to the game closest to my house is going to be optimal. But what if their opposition - the away team - is from a very long way away? There’s a 25% chance that “Faraway FC” will beat my local heros, become “my team” and then be drawn at home in the next round, leading to significant travel. “Faraway FC” might go on a cup run and get home draws all the way: I’d end up schlepping there every round. Perhaps there is some threshold, above which it actually makes sense to travel a bit further for the first match, to a fixture between two teams, both of whom are close-ish to home. Attending that fixture gives me a 50% chance of being quite close to home in the next round, because one or other will win and could be drawn at home.

Think of the probability tree for one of the semi-finals (When I drew these trees I adopted R₋₁ as a notation for semi-finals; R₀ would be the final). H means the team drawn at home in this semi, A their travelling opponents. X means the winner of the other semi-final. The winner of the semi we are focusing on (either H or A) can be at home or away in the final (remember we are ignoring the fact that finals are played at a neutral venue)??

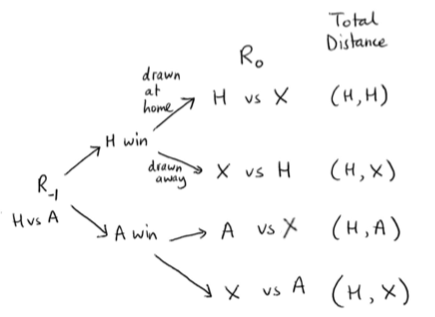
The itinerary then is, with equal probability: (H, H), (H, X), (H, A), or (H, X) and my expected travel cost is (5h + a + 2x) / 4, where:

• h means the travel cost to H’s ground
• a means the travel cost to A’s ground and
• x means the travel cost to X’s ground. We can take the mean travel cost of other potential opponents, since they occur with equal probabilities at this point in the tree *

* something about this makes my statistical spidey-sense tingle. I’m not an expert in this stuff. Anyway it makes it possible to carry on.

It’s easy to compute the expected travel cost for each semi-final, and decide which is optimal. I think in this small model, going to whichever semi-final is closer to home will always be optimal. Pleasingly, that isn’t the case for earlier rounds of this idealised version of the cup… here’s the tree for quarter finals.

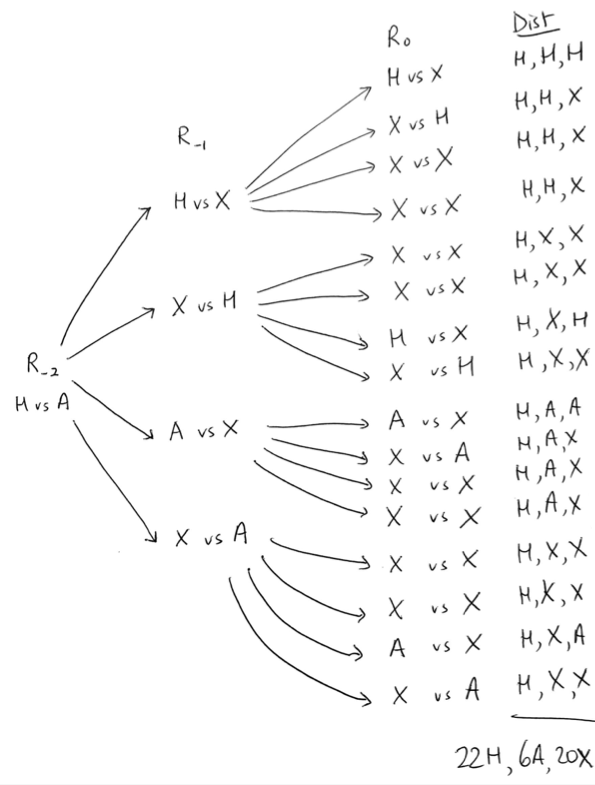
We get an expected travel cost of (22h + 6a + 20x) / 16. I haven’t drawn/couldn’t draw the tree for the next round, but with a bit of programming I reckon I can make a python script do it.

The results are:

• (5h + 1a + 2x) / 4 (semi-finals)
• (22h + 6a + 20x) / 16 (quarter-finals)
• (92h + 28a + 136x) / 64 (5th round, 16 teams)
• (376h + 120a + 784x) / 256 (4th round, 32 teams)
• (1520h + 496a + 4128x) / 1024 (3rd round, 64 teams)

Putting it all together into a little simulation, I can randomly sprinkle fixtures onto a canvas, and calculate these numbers, then highlight the optimal fixture. In the video below, orange square is “my house”, green squares are home teams' locations and away teams' locations are the other end of the grey lines. I picked the 4th round with 32 teams to play with. Travel cost is just the distance to the home games in pixels. Moving things around and trying things out, I can see that the optimal fixture is - as intuitively expected - often the one closest to home. Then at some threshold, my algorithm picks a fixture further away.

That’s probably enough for now. In the time I’ve been writing this blog post - spread over a few evenings - Liverpool and Stevenage have both been knocked out of the FA Cup. In a parallel universe, if they’d both won their fixtures this weekend, they would’ve met in the 5th Round!

Tags: geeky, football

< Previous post | Next post >